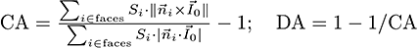You are here: Specialized Workflows > Bone Analysis > Computing and Visualizing Mappings of Anisotropy and Volume Fraction

Computing and Visualizing Mappings of Anisotropy and Volume Fraction

Computing and mapping surface and volume anisotropy by magnitude and orientation as vector fields and volume fraction as scalar values can help identify heterogeneity and latent features to correlate form with function in bone specimens. The options for computing anisotropy maps with the MIL and Surface normals algorithms, as well as for computing volume fraction, are available in the Bone Analysis dialog. Visualizations of vector-based maps are available in the 3D views in the workspace, while the mapped scalar values of volume fractions can be examined in both 2D and 3D views.

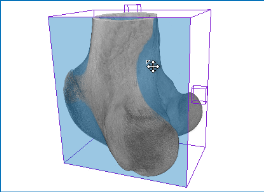
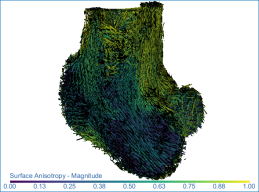
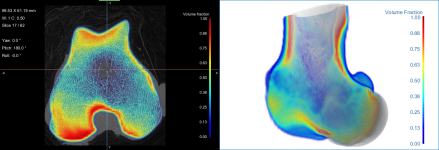
Surface anisotropy magnitude (left) and orientation (middle) and volume fraction (right) of a proximal femur

Several studies show that the degree of anisotropy, a description of how the structural elements are oriented, together with bone volume fraction may explain a significant part of the mechanical properties of a 3D structure. Refer to the application note Trajectories of Human Trabecular Bone Adaptation within a 4D Landscape of Tissue Anisotropy for information about evaluating mappings of anisotropy and volume fraction.

Mappings Methods and Settings

Two mapping methods — MIL and Surface normals — are available in the Bone Analysis module for computing anisotropy, as well as the option to generate scalar-based maps of volume fraction. These mapping methods are described below.

MIL… This classic method of anisotropy measurement using the Mean Intercept Length (MIL) method combines both surface and volume anisotropy components and requires sampling volumes to be about 4-5 inter-trabecular spaces.

The MIL algorithm can provide good information for evaluating orientation, but anisotropy values of magnitude can be overly noisy.

Surface normals… The surface anisotropy measurement exclusive to Dragonfly is based on the construction of a surface mesh populated by a set of vectors perpendicular to the mesh faces with their magnitude being proportional to the local mesh face area. For each anisotropy evaluation point, the faces having their center at a distance smaller than the radius of influence are identified. A tensor of inertia is constructed using the normals of these faces, linearly weighted by their area and weighted on their distance to the evaluation point by the function: w(d) = 1 - (d²)/(r_max²). The eigenvectors and eigenvalues of the tensor of inertia are obtained. The eigenvector corresponding to the greatest eigenvalue, corresponding to the smallest moment of inertia (maximal elongation) is taken as the anisotropy orientation.

The Projection-based algorithm computes anisotropy as:

, where CA is the coefficient of anisotropy, S is the local mesh face area, n is the normal to the face, I_O is the anisotropy orientation, DA is the degree of anisotropy. DA is a measure of how highly oriented substructures are within a volume. For an isotropic (perfectly oriented) system, the degree of anisotropy is equal to 0. As the system becomes more anisotropic (less well-oriented), the DA increases to some value less than or equal to 1.

The Eigenvalue-based algorithm gets anisotropy from the eigenvalues of the tensor of inertia, which is similar to the MIL algorithm.

The surface normals algorithm can provide very good general orientation information as well as high-resolution anisotropy values. For computations with the surface normals algorithm, the radius of influence can be as small as the size of a single trabeculae.

Volume fraction… The computed output is the proportion of the sample volume that is mineralized bone, in which a scalar value — 1 for high and 0 for low — is assigned to every spatial position (labeled voxel) in the input region of interest.

Global Settings

The global settings for computing mappings are described in the table below.

Global settings
	Description
Area box	Defines the analysis area for computing the selected mapping `(areaOfAnalysisBox)`. The initial box shape can be resized and/or reoriented as required (see Adding and Editing Shapes). RECOMMENDATIONS In cases in which you need very precise measurements and plan to use a small spacing value, you should reduce the area box as much as possible. You can also add multiple boxes to compute anisotropy and volume fraction maps in different orientations.
Spacing	Determines the distance between the random points in the analysis area `(areaOfAnalysisSpacing)`. Use single voxel in direction with smaller box length… If checked, computations will limited to a single voxel in the direction of the smallest length of the selected area box `(useSingleVoxelInDirectionWithSmallerBoxLength)`. This results in fast processing times and a simple vector field that is easy to evaluate, as shown below.

Algorithm Settings

The settings available for each mapping method are described in the table below.

MIL Settings

The settings for the MIL algorithm are listed in the table below.

Settings for MIL
	Description
Sampling	The resolution, or distance between subsequent samples along each vector `(samplingDistance)`. RECOMMENDATIONS The entered value should be about 4-5 inter-trabecular spaces.
Radius	The radius of the sampling sphere, which determines the length of each sampling vector `(lengthToAnalyze)`.
Orientations	The number of lines to analyze per sampling sphere`(countOrientations)`.

Surface Normals Settings

The settings for the Surface normals algorithm are listed in the table below.

Settings for Surface normals
	Description
Neighors	The Radius of Influence defines the kernel size, or elementary volume, within which anisotropy will be evaluated `(radiusOfInfluence)`. You should note that a too small radius of influence may result in a low signal-to-noise ratio, while a too high radius can result in averaging and edge effects. RECOMMENDATIONS The radius of influence can be as small as the size of a single trabeculae.
Anisotropy evaluation	Lets you choose an anisotropy evaluation method — Projection-based or Eigenvalue-based. You should note that both methods provide similar results, although you may find that the Projection-based method is slightly more sensitive.
Mesh smoothing (repetitions)	Determines number of times that the mesh obtained from the input ROI will be smoothed before computing anisotropy `(meshSmoothingRepetitions)`. RECOMMENDATIONS Selecting one or two iterations of smoothing usually provides for the most accurate result.

Volume Fraction Settings

The settings for the Volume fraction algorithm are listed in the table below.

Settings for Volume fraction
	Description
Radius	The distance from the analysis point to the last considered ROI element`(radius)`.

Computing Mappings of Anisotropy and Volume Fraction

Mappings of anisotropy and volume fraction can be computed from bone segmentations within the area defined by a Box shape. The inputs can be any region of interest or mesh, while the outputs of anisotropy and volume fraction mapping computations include the following:

Anisotropy of… Scalar-based map of anisotropy (channelAnisotropyMapping).

Eigenvector max of… Orientation field of the eigenvector associated to the highest eigenvalue (vectorFieldEigenvectorMax).

Volume fraction of… Scalar-based map of volume fraction (channelVolumeFractionMapping).

How to Compute a Mapping of Anisotropy or Volume Fraction

Add a Box shape to the workspace and size it to the region in which you want to compute the required mapping as follows:
- Select the region of interest that will be the input for computing the mapping in the Data Properties and Settings panel, recommended.
- Click the Box shape in the Shapes panel.
- Make the shape visible by clicking its associated Eye icon in the Data Properties and Settings panel.
- Adjust the size and position of the shape, as required (see Editing Shapes for information about resizing, rotating, and repositioning shapes).
  NOTE In cases in which you need very precise measurements and plan to use a small spacing value, you should reduce the box as much as possible. You can also add multiple boxes to compute anisotropy and volume fraction maps in different orientations.
- Lock the shape by checking the Locked option in the Visual effects box, recommended.
Choose Tools > Bone Analysis on the menu bar to open the Bone Analysis dialog.
Navigate to the Compute scalar and vector fields screen by clicking the Next button at the bottom of the dialog.
Select a mapping method in the Algorithm drop-down menu (see Mappings Methods and Settings).
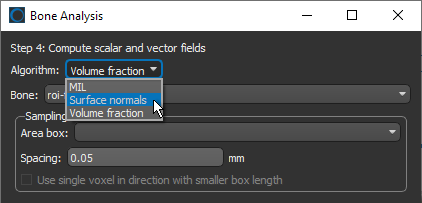
Select the region of interest or mesh that you want to map in the Bone drop-down menu.
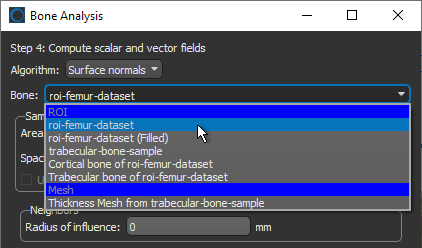
Select the Box shape that defines the region in which you want to compute the mapping in the Area box drop-down menu.
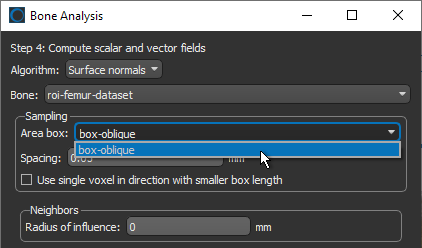
Enter the required spacing value in the Spacing edit box (see Global Settings).
NOTE For faster computations, and to obtain orientation fields that are easier to observe, you can select the Use single voxel in direction with smaller box length option. In this case, computations will limited to a single voxel in the direction of the smallest length of the selected area box.
Enter the required settings for the selected algorithm (see Algorithm Settings).
Click the Compute scalar and vector fields button to start the computation.
This will map the anisotropy of 3D surfaces — their preferred orientation and the direction of that preferred orientation with respect to the Cartesian coordinates — or the volume fraction.
At the end of the process, the requested vector field and/or generated dataset will appear in the Data Properties and Settings panel.
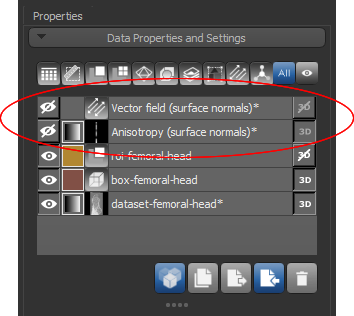
Continue to the next section to learn how to view vector fields and mappings of volume fraction.

Visualizing Mappings of Anisotropy and Volume Fraction

Visualizations of vector-based maps are available in the 3D views in the workspace (see Visualizing Vector-Based Maps of Anisotropy), while the scalar-based maps of volume fraction datasets can be evaluated in 2D and 3D views (see Visualizing Volume Fractions).

Visualizing Vector-Based Maps of Anisotropy

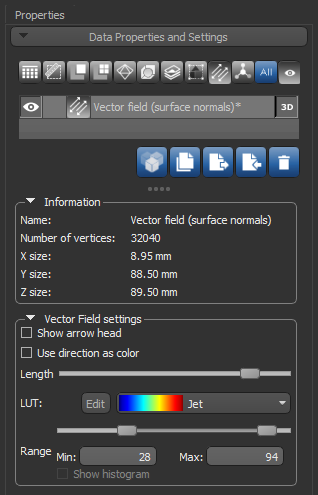
Settings for visualizing vector-based maps in 3D views, as well as basic information about a selected object, are available in the Data Properties and Settings panel, shown below.

Vector field properties and settings

Vector field properties and settings

Information for vector fields
	Description
Name	Indicates the name of the selected vector field.
Number of vertices	Indicates the total number of vertices in the computed surface mesh.
X size	indicates the dimension of the selected vector field in the X axis.
Y size	indicates the dimension of the selected vector field in the Y axis.
Z size	indicates the dimension of the selected vector field in the Z axis.

The following settings are available for adjusting visualizations of vector fields.

Vector-field settings
	Description
Show arrow head	If selected, arrow heads will appear on each vector in the field.
Use direction as color	If selected, each Euclidean vector will be colored according to its orientation — X in red, Y in green, and Z in blue. If not selected, each Euclidean vector will be colored according to the anisotropy value computed in the output anisotropy dataset. Coloring is selectable in the LUT drop-down menu.
Length slider	Lets you adjust the length of the Euclidean vectors in the selected vector field.
LUT	Lets you select the colors that will be applied to mapped anisotropy values. NOTE This option is not available whenever the Use direction as color option is selected.
Range	Lets you threshold the minimum and maximum values that are displayed.